Two of the Most Beautiful Songs in the World

It always helps to know how to keep the mind in a positive frame.
Here are two of the very best songs in the world.

What a Wonderful World
by
Louis Armstrong



Downtown
by
Petula Clark

The big metallic egg / bean mirror sculpture in this video sits in a park in downtown Chicago.
It was designed by a British-Indian artist Anish Kapoor.

Operations

If a periodic (ordered) function operates upon a chaotic (random) function, is the resulting function ordered or chaotic?
If we choose a periodic function such as sin(x), and let x be a random (chaotic) number from -infinity to +infinity. Can a prediction be made about the result? Yes. The result will never exceed 1 in magnitude. But that's it. No other prediction can be made about the resultant numbers.
Now we can try the reverse, and try to choose a random function that takes its seed from a periodic function. Here, we run into a problem. A truly random function that is calculated using arithmetic does not exist. But we can get close to true randomness by proper choice of seeds for the random number generator. In principle, therefore, an operation of randomness on a seed of periodic nature, will produce randomness.
Thus, it appears that the operand loses its qualities to the operator. An ordered function operation produces limits to randomness, and a chaotic operation makes the periodic seed lose its predictability.

Order and Chaos

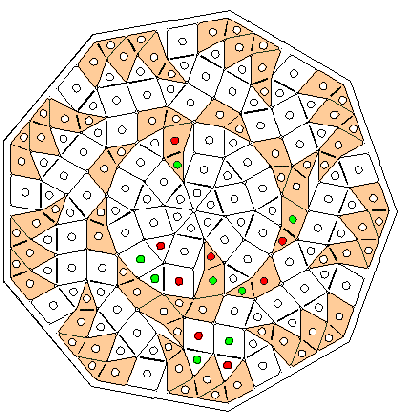
Is there any discernible pattern in this figure? (from http://www.mathpuzzle.com/)

What distinguishes order from chaos? In one word, symmetry. Symmetry implies predictability. Symmetry implies a lower energy configuration of the constituent units. Symmetry implies stability. However, stability and lower energy configuration are relative terms, and only stay true as long as the reference is to complete chaos.

Thus, to understand order, one needs to understand symmetry at the most basic stable level of organization in this universe - the atom and the molecule. There are structures at sub-atomic levels, of course, but we need not worry about those here for the most part.

Contrary to what most people might think, the atoms are not generally isotropic in their structures or properties. Atomic orbitals come in different shapes and sizes (see here). The other constraint to take into account while calculating atomic interactions (that produce symmetry configurations), is the nature of space. Only three directions in space are independent of each other (Cartesian geometry - expanded). How many freedoms does that leave the atoms (or any other unit) with, in order to form an inter-atomic structure?

[By the way, do read the life and works of René Descartes (1596-1650), after whom the Cartesian co-ordinates are named - his genius cannot be truly appreciated until you read his original and complete works, such as the nature of things.]

Surprisingly, although atoms can aggregate in a vast number of ways to form molecules (each new atom added changes the molecule), molecules can only aggregate in a fixed number of ways to form crystals (as do pure elements when solidified through crystallization). In three dimensions, there are only 14 shapes that a unit cell of a crystal can order itself in - these are called Bravais Lattices.

What does all this have to do with order and chaos? We will continue with this argument in the next post!